Nearly Tight Bounds for Exploration in Streaming Multi-armed Bandits with Known Optimality Gap

We investigate the sample-memory-pass trade-offs for pure exploration in multi-pass streaming multi-armed bandits (MABs) with the *a priori* knowledge of the optimality gap $\Delta_{[2]}$. Here, and throughout, the optimality gap $\Delta_{[i]}$ is defined as the mean reward gap between the best and the $i$-th best arms. A recent line of results by Jin, Huang, Tang, and Xiao [ICML'21] and Assadi and Wang [COLT'24] have shown that if there is no known $\Delta_{[2]}$, a pass complexity of $\Theta(\log(1/\Delta_{[2]}))$ (up to $\log\log(1/\Delta_{[2]})$ terms) is necessary and sufficient to obtain the *worst-case optimal* sample complexity of $O(n/\Delta^{2}_{[2]})$ with a single-arm memory. However, our understanding of multi-pass algorithms with known $\Delta_{[2]}$ is still limited. Here, the key open problem is how many passes are required to achieve the complexity, i.e., $O( \sum_{i=2}^{n}1/\Delta^2_{[i]})$ arm pulls, with a sublinear memory size. In this work, we show that the ``right answer'' for the question is $\Theta(\log{n})$ passes (up to $\log\log{n}$ terms). We first present a lower bound, showing that any algorithm that finds the best arm with slightly sublinear memory -- a memory of $o({n}/{\text{polylog}({n})})$ arms -- and $O(\sum_{i=2}^{n}{1}/{\Delta^{2}_{[i]}}\cdot \log{(n)})$ arm pulls has to make $\Omega(\frac{\log{n}}{\log\log{n}})$ passes over the stream. We then show a nearly-matching algorithm that assuming the knowledge of $\Delta_{[2]}$, finds the best arm with $O( \sum_{i=2}^{n}1/\Delta^2_{[i]} \cdot \log{n})$ arm pulls and a *single arm* memory.

Collaborative Regret Minimization in Multi-Armed Bandits

In this paper, we study the collaborative learning model, which concerns the tradeoff between parallelism and communication overhead in multi-agent reinforcement learning. For a fundamental problem in bandit theory, regret minimization in multi-armed bandits, we present the first and almost tight tradeoffs between the number of rounds of communication between the agents and the regret of the collaborative learning process.

Communication-Efficient Collaborative Best Arm Identification

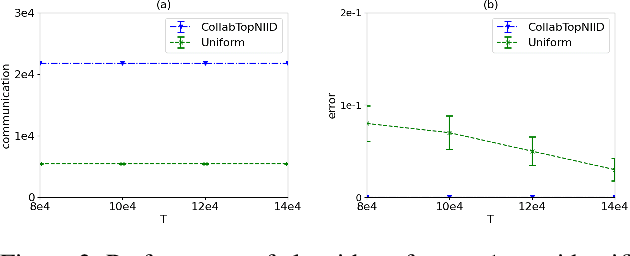
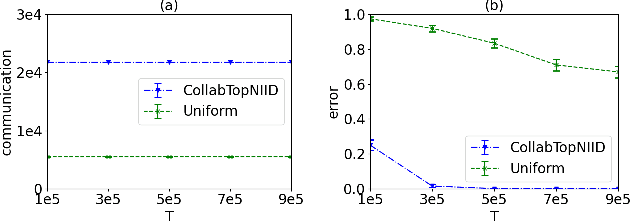
We investigate top-$m$ arm identification, a basic problem in bandit theory, in a multi-agent learning model in which agents collaborate to learn an objective function. We are interested in designing collaborative learning algorithms that achieve maximum speedup (compared to single-agent learning algorithms) using minimum communication cost, as communication is frequently the bottleneck in multi-agent learning. We give both algorithmic and impossibility results, and conduct a set of experiments to demonstrate the effectiveness of our algorithms.

Collaborative Best Arm Identification with Limited Communication on Non-IID Data

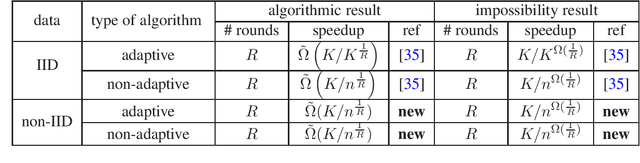
In this paper, we study the tradeoffs between time-speedup and the number of communication rounds of the learning process in the collaborative learning model on non-IID data, where multiple agents interact with possibly different environments and they want to learn an objective in the aggregated environment. We use a basic problem in bandit theory called best arm identification in multi-armed bandits as a vehicle to deliver the following conceptual message: Collaborative learning on non-IID data is provably more difficult than that on IID data. In particular, we show the following: a) The speedup in the non-IID data setting can be less than $1$ (that is, a slowdown). When the number of rounds $R = O(1)$, we will need at least a polynomial number of agents (in terms of the number of arms) to achieve a speedup greater than $1$. This is in sharp contrast with the IID data setting, in which the speedup is always at least $1$ when $R \ge 2$ regardless of number of agents. b) Adaptivity in the learning process cannot help much in the non-IID data setting. This is in sharp contrast with the IID data setting, in which to achieve the same speedup, the best non-adaptive algorithm requires a significantly larger number of rounds than the best adaptive algorithm. In the technique space, we have further developed the generalized round elimination technique introduced in arXiv:1904.03293. We show that implicit representations of distribution classes can be very useful when working with complex hard input distributions and proving lower bounds directly for adaptive algorithms.

Batched Thompson Sampling for Multi-Armed Bandits

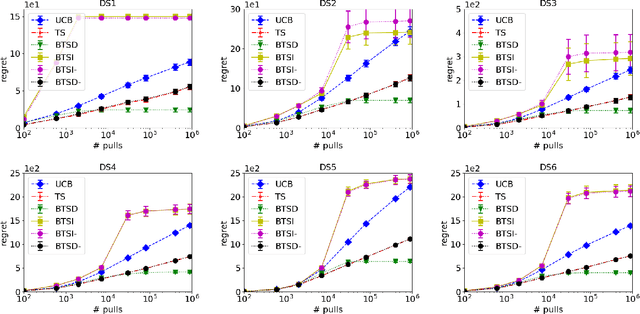
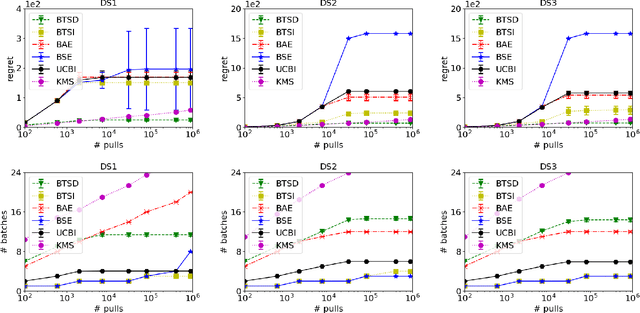
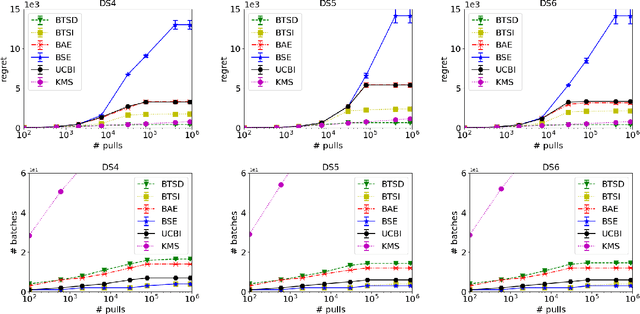
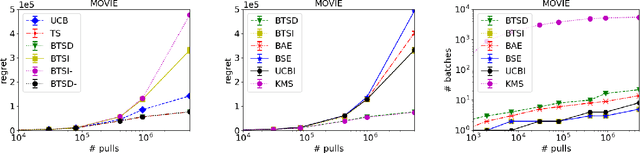
We study Thompson Sampling algorithms for stochastic multi-armed bandits in the batched setting, in which we want to minimize the regret over a sequence of arm pulls using a small number of policy changes (or, batches). We propose two algorithms and demonstrate their effectiveness by experiments on both synthetic and real datasets. We also analyze the proposed algorithms from the theoretical aspect and obtain almost tight regret-batches tradeoffs for the two-arm case.

Instance-Sensitive Algorithms for Pure Exploration in Multinomial Logit Bandit

Motivated by real-world applications such as fast fashion retailing and online advertising, the Multinomial Logit Bandit (MNL-bandit) is a popular model in online learning and operations research, and has attracted much attention in the past decade. However, it is a bit surprising that pure exploration, a basic problem in bandit theory, has not been well studied in MNL-bandit so far. In this paper we give efficient algorithms for pure exploration in MNL-bandit. Our algorithms achieve instance-sensitive pull complexities. We also complement the upper bounds by an almost matching lower bound.

Collaborative Top Distribution Identifications with Limited Interaction

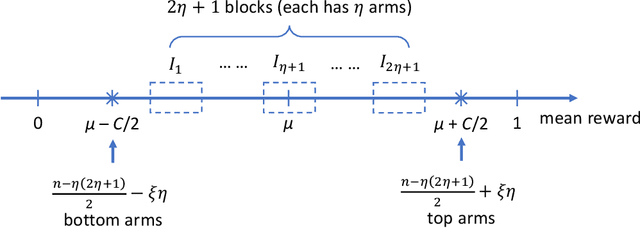
We consider the following problem in this paper: given a set of $n$ distributions, find the top-$m$ ones with the largest means. This problem is also called {\em top-$m$ arm identifications} in the literature of reinforcement learning, and has numerous applications. We study the problem in the collaborative learning model where we have multiple agents who can draw samples from the $n$ distributions in parallel. Our goal is to characterize the tradeoffs between the running time of learning process and the number of rounds of interaction between agents, which is very expensive in various scenarios. We give optimal time-round tradeoffs, as well as demonstrate complexity separations between top-$1$ arm identification and top-$m$ arm identifications for general $m$ and between fixed-time and fixed-confidence variants. As a byproduct, we also give an algorithm for selecting the distribution with the $m$-th largest mean in the collaborative learning model.